機械学習でダメ絶対音感を再現する ~機械でウマ娘声優予想はできるのか~
こんにちは、tube_worm です。
さて、唐突ですがぼくは声優の相坂優歌さんを応援しています。この相坂優歌さんが参加しているプロジェクトにウマ娘というものがあります。簡単に言うと競走馬の擬人化です。詳細は公式サイトを見てください(自分も詳細はよくわからない)。
このウマ娘なのですが、すでに18キャラクターが公開されており、それぞれのソロ曲やユニット曲なども発売されています。これはブログの本筋とは関係ないのですが、相坂優歌さん演じるナリタブライアンのソロ曲「シャドーロールの誓い」がクッソエモいのでオタクは聴け。これはマスト*1。
さて、本筋に戻りますと、この18キャラ以外に追加で41キャラクターが、元ネタとなった競走馬(すなわちキャラクターの名前)のヒント・サンプルボイスともに公開されています。正解発表は7/1のイベントで行われるということです。今日ですね。はい、ぎりぎりです。
ここでオタクのみなさんは思いつくのではないでしょうか?
「サンプルボイス公開されてるなら CV 当てられるんじゃね?」
そう、ダメ絶対音感というやつです。
しかしここでぼくはこう考えてしまいました。
「普通にオタクがサンプルボイス聞いて CV 予想するだけじゃただのオタクだよな~」残念なくらい逆張りです。というかオタクじゃないので全然 CV 予想つきません。耳が腐っている。いや25番が藤田茜さんとかはさすがにわかるけど*2。→外してたので耳を削ぎ落しました。
というわけで今回の趣旨です。
「機械学習を用いて、未知のキャラクターボイスから声優の判別ができる判別機『声豚くん』は作製できるのか?」
流れ
結果
声豚くんはダメダメでした。
流れの一つ目、既知のキャラ判別がまずボロボロだったので追加キャラの予想は諦めました。……結果としてはうまく判別できなかったのですが、「はい、うまくいきませんでした、おわり」では身も蓋もないのでまあ今回とりあえずできたこと、結果と改善点なんかを適当に述べていきたいかと思います。
なにはともあれ結果です。

縦軸にキャラクター名、横軸に声優名をとって、それぞれのキャラクターがどれくらいの確率でどの声優に判定されたかをプロットしています。本来のCVが正確に予測できていれば左上から右下にかけて対角線上に濃いプロットとなるはずですが……う~~ん、微妙。
教師データ
特徴量など詳細は以降の記事に任せますが、まずは学習用の教師データが必要です。教師データとはすなわち声豚くんに対して「この声は声優の~~の声だよ」と教えてあげるものです。声豚くんはこの教師データを元にして未知の声を分類していきます。声豚くんを一人前の声優オタクに仕上げましょう。
今回は教師データとして、声優事務所のサンプルボイスを使いました。前田玲奈さんはサンプルボイスがなかったので、前田玲奈さん演じるグラスワンダーは使用しませんでした。
「エロマンガ先生」五話のオタクが走るカットについて考える
※ぼくは世界史を本当にかじった程度でしか知らないので誤った記述を含む可能性があります。
「今日も疲れたな~~~」
帰り道で一杯ビールをひっかけて気分が良くなったぼく。帰宅してから録画リストを見て観るアニメを決めます。
「エロマンガ先生で知能2にして寝るか~~~~~~」
再生。
「紗霧ちゃんかわい~~~」
「山田エルフ先生のぱんつってどんな味がするのかな~~~~」
ん?
「このカットなんだ?????」
そうです、途中で何度か挟まれる太った男性が土手を走るカットのことです。皆さんも気になったかと思います。ぼくは気になりすぎてずっとそのことを考えていたら寝られなくなりました*1。
あの男性はダイエットをしているのか?
なぜ最後に倒れるのか?
一体何のメッセージがあるのか?
彼はマラソンでもしているのか?
……ん、マラソン?
マラトンの戦い
さて、「マラソン」という言葉の語源についてはそこそこ有名なので知っている人も多いかと思います。紀元前490年、当時オリエント世界を統一し圧倒的な勢力を誇っていたアケメネス朝ペルシアは「王の道」整備で知られるダレイオス一世の指揮のもと、ギリシア制服を目論み、イオニアで起きたペルシアに対する反乱へのアテナイ(アテネ)の加担を口実に攻め立てます。しかしアテナイとアテナイに加担したプラタイアはこれを返り討ちにし勢力を拡大させます。アテナイ側の勝利に終わったこの戦いがマラトンの戦いです。
このマラトンの戦いの勝利を報告するため、ある歩兵がマラトンからアテナイまでのおよそ40 kmを駆け抜け、「我ら勝てり」と伝え絶命したとヘロドトスの「歴史」には書いてあり、これがマラソンの起源だとされます。*2*3*4
エロマンガ先生とマラトンの戦い
さて、話が相当脇道にそれましたが、僕は世界史の話をしたくて筆を執ったわけではありません。エロマンガ先生の話がしたかったのです。*5
エロマンガ先生五話の土手を走る太った男性(長いので「オタク」と呼びます)、このオタクの走るカットが五話の途中で何度か挟まれます。そして主人公の和泉マサムネが紗霧ちゃんの描いた絵を見て
「これからもよろしく頼むぜ、エロマンガ先生」
「そんな名前の人知らない」
という いつもの茶番 圧倒的名シーン の後、このオタクの最後のカットが挟まれます。このカットに今までと異なる点が存在します。
そう、勘のいいみなさんならもうお気づきでしょう。
このオタク、倒れるんです。
これはマラトンの戦いの勝利を伝えた歩兵そのものなのでゎ!?!?!?!?!?
では、彼は一体誰の勝利を伝えるためあんなに必死になって走っていたのでしょう?
それを考えるうえで重要になるのが彼の外見です。
彼はオタクです。360度どの角度から見てもオタクです。可哀想。
そんなオタクの濃縮還元ジュースみたいな見た目の彼が伝える勝利、それはオタクの勝利に他なりません。そう、それは視聴者の勝利です。そしてオタクである視聴者が最も感情移入するであろう和泉マサムネの勝利なのです*6。そう、エロマンガ先生が妹であると気付いてから初めての共同作業、その企画書を書き上げる一歩目を踏み出すことができた、その「勝利」なのです。
長々と書いてきましたが、最後にぼくがこの記事で最も伝えたかったこの言葉と共に〆させていただきます。
今期覇権はロクでなし魔術講師と禁忌経典!
三本立て、読む価値のない雑記
お久しぶりです。tube_worm です。なんと9ヶ月以上も更新していなかったらしく、さすがに放置しすぎたなと思い筆を、もといキーボードを執った次第です。下書き欄を覗いてみると、投稿されなかった雑多な下書きがたくさん埋もれています。この9ヶ月間で考えたことの一部を、少しだけ継ぎ接ぎで無理矢理一つの記事としてしまおうと思います。まあこのブログを読んでいる人なんて数が知れているでしょうし、読みやすさなど気にせず、気の向くままに書き殴りました。
「四畳半神話大系」を観て【ネタバレを含みますので未視聴の方は飛ばしてください。】
「夜は短し歩けよ乙女」の映画化で話題になっていますね。先に断っておきますがこの映画は観ていないです。
「四畳半神話大系」を観たのは5か月ほど前でしょうか。全体的な感想としては、細かい演出は面白かったのだけど、最終的なオチというか、結末がいまいちしっくりこなかったという感じです。
前半はずっと、大学生になって所謂「キャンパスライフ」を満喫しよう、というところから始まります。個人的に思うところも多く、非常に共感できる部分が大きい出だしとなりました。
しかし転機は9話に訪れます。悪友であった小津に「恋人がいる」ということに主人公である「私」が衝撃を受ける、というところあたりから物語の歯車と僕の持つ歯車が噛み合わずに狂ってきます。「四畳半神話大系」に限らず、大学生を描くにあたって、「恋人の存在」がある種ステータスとして、幸せの象徴として、「普通の大学生活」の象徴として描かれることが多いと(少なくとも僕は)感じるのですが、これに異常な違和感を覚えます。ただ単にステータスの一つとしてならまだ理解はできるのですが、ある種絶対的な、代替不可能なステータスとして「恋人の存在」が描かれてしまうと、僕の持つ価値観との相違が気になってしまいます。「四畳半神話大系」においては、その差異によって主人公である「私」との共感がとても薄れてしまいました。9話までは「私」の抱く感情にとても共感しており、また主人公を「私」としてあえて名前を与えないというレトリックの恩恵を大いに受け、僕個人の経験や価値観と擦り合わせ観ていたのですが、この9話の描写以降共感が酷く薄れてしまい、とても冷めた気持ちで観てしまいました。主人公たる「私」と視聴者たる僕との乖離が激しくなってしまい、意味不明なまま気付けば最終話が終わっていました。
「NEW GAME!」を観てパニック障害になった話
タイトル通りの話です。「NEW GAME!」の一話を観たときに、オフィスで皆が働いているシーンでなぜか心拍数が以上に上がり冷や汗が噴き出てきて視聴継続が困難になった、それだけの話です。
「いや、これ時間通りに出勤する意味ってなに」「そもそも外部に活動時間を規定されるのが本当に無理な自分にとって意味がわからない」「なんで働くの?」「なんでこのキャラクターたちは僕の持つ数々の疑問を1つも抱かずに社会に飼いならされているの」といった疑問が一気に湧き出てきて普通にパニック障害になりました。原作を読んだときはこんなこと一切なかったので普通にビビりました。すぐにトイレに駆け込んで嘔吐し視聴を断念しました。いつか僕にもこのアニメを平常心で観られる時が来るのでしょうか。
アニメに全然関係ないとても短い話
さて、唐突ですが僕はタバコを嗜みます。よく「このご時世に」「体に悪い」「あそこにベンツが停まってますね」などと言われます。
僕にとってタバコは日常に打ち込む楔です。毎日決まった時刻に起床し、決まったルートで決まった場所に行き、決まったことを行い、決まった定型句で形だけの会話をする。二枚舌。皆さんはそんな平日という連続した虚無、休日という仮初の実存から離れた虚無を生きてはいませんか?(休日がないという方はご愁傷様です。)それは「生きて」「過ごして」「暮らして」はいても「活きて」はいないのではないですか?
もう月曜日です。今日のタバコは少し苦いです。
Barabasi-Albert アルゴリズムの実装
[Background]
C90 に向けての原稿を書くためにネットワークの勉強をしています。東京大学性欲研究会というサークルで日曜日東ピ24aにブースを出すのでよければお願いします。
さて、この原稿で使う Barabasi-Albert アルゴリズムというアルゴリズムがあり、その実装を行ったのですが、まず背景から説明したいと思います。ちなみにこのアルゴリズムがどう原稿に使われているかはお楽しみです。
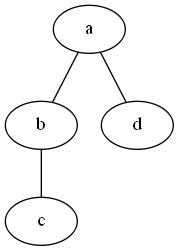
まずネットワークの構造について説明します。ここで言うネットワークは"グラフ"という言葉 (円グラフや棒グラフのグラフではなくグラフ理論のグラフです。後ほど説明します。) とほぼ同義だと思ってください。グラフとは、"ノード" (頂点) と"エッジ" (辺) からなる構造で、ノード間にエッジが張られています。このエッジがノード間のつながりを表すと思って良いと思います。今回は関係ありませんが、このエッジに"重み"という値がついている場合もあります。イメージとしては、駅がノードで、駅間のエッジが路線とすると、所要時間を重みとして与えることで路線図のグラフができる、みたいなもので良いと思います。 Wikipedia によるとグラフの中でも重みつきのものをネットワークと呼ぶようですが、少なくともここでは区別しません。とりあえず、ノードとエッジとだけ把握しておいてください。
さて、各ノードについて、そのノードからエッジが何本でているかという値が取れます。この「何本エッジが出ているか」をそのノードの"次数"といいます。たとえばノードの間に引くエッジをランダムに選んだとすると、この次数の分布を考えると二項分布になります (めんどくさいので細かい説明は省きます。気になる人は Wikipedia でも見てください、すみません) 。
 二項分布の例、Wikipedia から引用
二項分布の例、Wikipedia から引用
ここで、実際の世界によく現れるネットワーク構造について考えてみます。たとえばインターネットウェブのネットワークや、生態学における捕食・被食関係、友人関係などです。これについて次数の分布を見てみると、実際には二項分布でなく、べき分布という形になっていることが知られています。
 べき分布の例、Wikipedia から引用
べき分布の例、Wikipedia から引用
 指数分布の例、Wikipedia から引用
指数分布の例、Wikipedia から引用
このように次数分布がべき分布となるようなネットワークのことを"スケールフリーネットワーク"と呼びます。「次数分布がべき分布」といわれても何のことかわかりにくいのですが、要は「次数の低いたくさんのノードと、少数の次数の高いノードが存在する」ということです。この次数の高いノードのことを"ハブ"と呼びます (ハブ空港などのハブです) 。この少数のハブが、大多数の次数の低いノードとエッジを張っててネットワークが構成されているというイメージです。このネットワークの特徴として、ランダムにノードをつぶすような攻撃に対して強いというものがあります。スケールフリーネットワークに存在するノードは大多数が低次数のノードなので、この攻撃によってランダムにつぶされるノードはほとんどが次数の低いノードとなり、ネットワークの構造が保たれやすいためです (もちろん、たまたま少数のハブがつぶされた場合には崩壊しますが、それは確率的には起こりにくいものです) 。このため、たとえばインターネットウェブは停電などでランダムにサーバーが落ちてしまうといった事故に強く、捕食・被食ネットワークではひとつの種が絶滅しても生き残りやすいといった強みがあります。
さて、では実世界に多いこのスケールフリーネットワークをシミュレーションで扱いたいと考えたときに、どうやって作るかという問題が生じます。ランダムネットワークでは、ノードを作ってランダムにエッジを張ってやればよいのですが、スケールフリーネットワークを作ろうと考えた場合そうはいきません。ここで出てくるのがタイトルにある Barabasi-Albert アルゴリズムです (タイトル回収まで長かった……) 。
このアルゴリズムの概要を説明すると、まず少ないノード数 m0 (今回のシミュレーションでは2つ) で"完全グラフ" (全てのノード間にエッジが張られているグラフ、今回は2ノードなのでただの線分です) をつくります。次に、ここにひとつずつ新しいノードを付け加えます。この新しいノードから、既存のノードに対して m0 以下の本数 (今回は1本) のエッジを張ります。ここでエッジが張られる確率を、その対象となるノードの次数に比例する、とするのが Barabasi-Albert アルゴリズムです。今回は新しいノードから一本だけエッジが張られるので、既存のノードからすれば自分のノードにエッジが張られる確率は
(自分の次数) / (既存のノード全ての次数の和)
となります。
直感的には、「すでにたくさんのノードが張られている "ハブ" 」についてはさらにエッジが張られやすいので、 "ハブ" の構造が維持されやすいということになります。
[Result]
1000個のノードを作ったグラフです。割ときれいにハブが存在するのが見えると思います。

200000個のノードでも作ってみましたが、さすがに大きすぎてグラフは載せられないので、次数に対してノードの数を取ったグラフを載せます。二枚目は縦軸・横軸ともにその log を取った両対数プロットです。
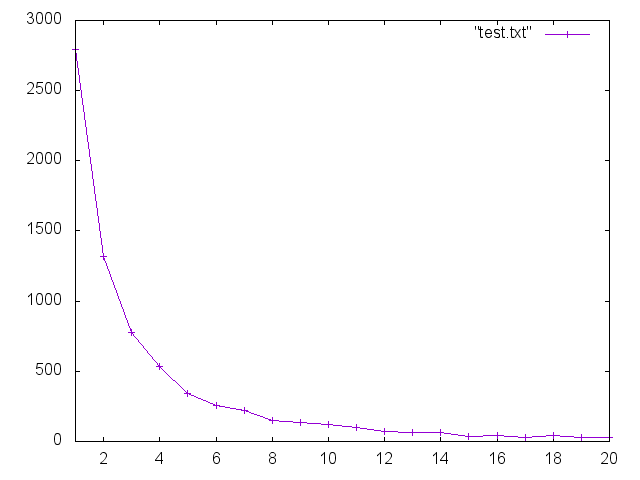
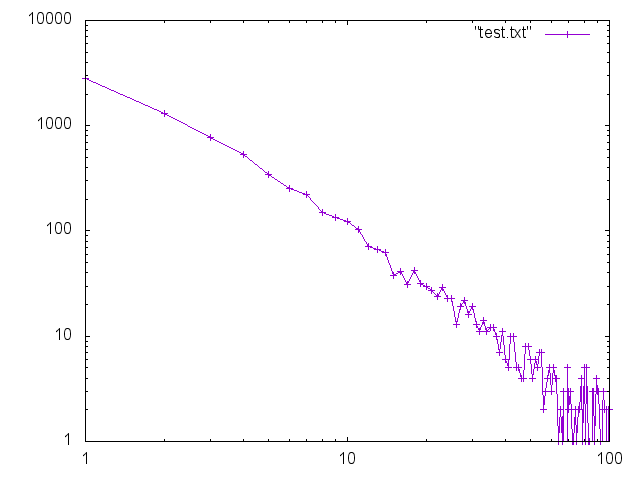
指数分布 (y = e^ax) でなくべき分布 (y = x^r) というかたちなので、ただ縦軸だけを log にしても直線にはなりません。 log(y) = r log(x) となるので両対数が正解です!二枚目が直線に近くなっているのでちゃんとスケールフリーネットワークになっていることが確認できます!
こうしてみてみるとグラフの見た目がなんとなく梅の花に見えますね。ここからは根拠のない妄想なのですが、梅の花は多分構造的にフラクタルなので次数分布がべき乗にのりそうで、グラフ化してみてみるとスケールフリーネットワークになっている、みたいなことがあるかも知れません。確かめてみると面白いかもしれませんね。
C90 では今回作ったハブの構造を持つネットワークを用いてごにょごにょいじったシミュレーションを行います。気になった方はぜひよろしくお願いします!!!!続きはビッグサイトで!!!!!!!!!!!
[追記!]
指数分布とべき分布とを混同していたので160717に訂正を加えました!訂正箇所は赤文字にしています。
[Code]
(10/25 追記) コード内の変数にある "order" は次数のつもりで使っていますが、"order" は「位数 (グラフの頂点数)」です。次数は "degree" です。訂正します。
#include <iostream> #include <vector> #include <algorithm> #include <fstream> #define N 200000 // the number of nodes #define MAXORDER 500 // maximum order a node can have using namespace std; struct node { int number; int order; vector<node*> adj; // vector of pointers to adjacent nodes void link(node&); }; void node::link(node& n) { adj.push_back(&n); n.order++; } void annual_link(node& n1, node& n2) { n1.link(n2); n2.link(n1); } struct population { node* list; // array of the nodes int ordersum; int size; }; #define N0 2 // initial number of complete graph for BA void BarabasiAlbert(population &population, int n) // the argument n is the number of nodes { int n0 = N0; population.list = new node[n]; /* start with complete graph */ for (int i = 0; i < n0; i++) population.list[i].order = 0; for (int i = 0; i < n0; i++) { population.list[i].number = i; for (int j = i + 1; j < n0; j++) annual_link(population.list[i], population.list[j]); } for (int i = 0; i < n0; i++) population.ordersum += population.list[i].order; population.size = n0; /* end of making complete graph */ /* add the nodes from n0-th to N-th */ for (int i = n0; i < n; i++) { population.list[i].order = 0; population.list[i].number = i; int r = rand() % population.ordersum; int k = 0; while (r >= 0) { r -= population.list[k].order; k++; } k--; annual_link(population.list[k], population.list[i]); population.ordersum += 2; population.size++; if (i % 100 == 0) cout << i << "is done!" << endl; } } #undef N0 /* population to dot format */ void dotoutput(ofstream ofs, population p) { ofs << "graph graph_name{ \n graph[\n" << endl; ofs << "dpi = \"480\", \n layout = sfdp\n ];" << endl; ofs << "node[\n shape = point,\n fillcolor = \"#FF0000\",\n color = \"#FF0000\",\n fixedsize = true, \n width = 0.02\n]; " << endl; for (int i = 0; i < p.size; i++) { for (int j = 0; j < p.list[i].order; j ++) if (i < p.list[i].adj[j]->number) { ofs << i << "--" << p.list[i].adj[j]->number << ";" << endl; } } ofs << "}" << endl; } #define SEED 1 int main() { srand(SEED); population population; population.ordersum = 0; population.size = 0; BarabasiAlbert(population, N); // check int order[N]; int ordernum[MAXORDER] = {}; for (int i = 0; i < N; i++) { order[i] = population.list[i].order; ordernum[order[i]] ++; } sort(order, order + N); ofstream ofs("test.txt"); ofstream logofs("log.txt"); for (int i = 1; i < MAXORDER; i++) { ofs << ordernum[i] << endl; logofs << log10(ordernum[i]) << endl; // the increment is for avoidance of negative infinity } dotoutput(ofstream("graph.dot"), population); return 0; }
Scheme で解く 8 queens puzzle
[Background]
現在友人三人と以下にある "Structure and Interpretation of Computer Programs" という本 (SICP と呼んでいます。いわゆる「魔術師本」) の日本語訳でゼミをしています。簡単に言うとプログラミング言語のひとつである LISP の方言である Scheme について書きながらアルゴリズムの設計の仕方やデータ構造についても説明がなされている本です。
練習問題の答えをメモ代わりに貼っているブログもあります。
sicp-zemi.hatenablog.jp
ここにある練習問題 2.42 がなかなか面白かったのでいろいろ遊んでみました。
まず問題は、 "8 queens puzzle" と呼ばれるもので、 8×8 マスのチェス盤の上に 8 個のクイーンを置くのですが、その 8 つのクイーンが互いに「利き筋に入らない」 (クイーンは行・列・対角線上を移動できるので、その道筋上に他のクイーンがいない) ような配置の仕方を考える、というものです。チェス盤の行・列の数とクイーンの数を n と一般化した問題を考えます。
では実際に、SICP の誘導どおりに解き方を考えます。
簡単に一言で説明しちゃうと、帰納法で解きます。つまり、まず k-1 列目まで、条件を満たすように k-1 個のクイーンが配置されていると仮定します。この条件の下で、 k 列目のどこにクイーンを置けばよいか考えます。 k 列目の 1 行目から n 行目、座標で表すと (1, k)~(n, k) のそれぞれについてクイーンを置いてみて、利き筋に入らないという条件を満たすか調べてみて、条件を満たすものだけを取り出す、こうすると k 列目までに k 個のクイーンが条件を満たして置かれた配置ができます。これを k = 1~n まで行えば完了というわけです。
SICP ではこれを解いて Scheme のデータ構造であるリスト表現を出力すれば終わりとなっているのですが、少し結果がわかりづらいので出力を可視化するコードも書いてみました。
[Code]
Scheme から派生した racket という言語で書いていますが、ほとんど Scheme と同じです。環境によっては "null" が定義されていないと怒られるかもしれないのでその場合は "(define null '())" を書き加えてください。
コードの細かい説明は全部コメントで書いておきました。
#lang racket ;accumulate: 初期値 initial から始めて、配列 sequence の要素を右から取って来て 2-ary operation の op に食わせていく感覚 (define (accumulate op initial sequence) (if (null? sequence) initial (op (car sequence) (accumulate op initial (cdr sequence))))) ;filter: 配列 sequence の中で、条件式 predicate を満たす要素だけを取り出してきて配列を再構成する (define (filter predicate sequence) (cond ((null? sequence) null) ((predicate (car sequence)) (cons (car sequence) (filter predicate (cdr sequence)))) (else (filter predicate (cdr sequence))))) ;flatmap: 元配列 seq の各要素に対して処理 proc を行ったものを append して返す (map だと append じゃなくて cons なので段差ができてしまう) (define (flatmap proc seq) (accumulate append null (map proc seq))) ;enumerate-interval: low から high までの公差 1 の数列を生成する (define (enumerate-interval low high) (if (> low high) null (cons low (enumerate-interval (+ low 1) high)))) ;初期状態 (ただの空リスト) (define empty-board null) ;adjoin-position: すでに配置されたクイーンの座標のリスト rest に座標 (row, col) をリストの頭に加える (define (adjoin-position row col rest) (cons (cons row col) rest)) ;safe?: 新しく加えられたクイーンが利き筋に入っていないか判定する ;列は k 番目の列なので問題ない、行と対角線を判定 ;safe?-sub は新しいクイーンの座標 p とすでに配置されていたクイーンの座標リスト rest とを引数にとり、 rest の頭から再帰的に判定 (define (safe?-sub p rest) (if (null? rest) #t (cond ((= (caar rest) (car p)) #f) ((= (abs (- (car (car rest)) (car p))) (- (cdr p) (cdr (car rest)))) #f) (else (safe?-sub p (cdr rest)))))) ;safe? の引数は今何列目にいるかをあらわす k と、新しいクイーンの座標が頭についたクイーンの座標リスト positions (define (safe? k positions) (let ((col (car positions))) (safe?-sub col (cdr positions)))) ;以下がメインになる部分 ;lambda (new-row) は、1 から n までの数列 (enumerate-interval) の各要素に対して adjoin を行う、つまり (1, k)~(n, k) の座標をすでにあるクイーンの座標リストに加える ;(queen-cols (- k 1)) がすでにある k-1 列目までのクイーンの座標リスト (ひとつの盤面に対応) のリスト (つまり盤面のリスト) 、それの各要素 (つまりひとつの盤面) に対して lambda (rest-of-queens) のラムダ閉包 (関数みたいなもの) を作用させることで、新しいクイーンの座標候補 (まだ条件を満たすかの判定をしていないので候補どまり) が加わった、新しい盤面のリストができる ;filter で条件を満たす盤面だけを取り出して k 列目までが完成 (define (queens board-size) (define (queen-cols k) (if (= k 0) (list empty-board) (filter (lambda (positions) (safe? k positions)) (flatmap (lambda (rest-of-queens) (map (lambda (new-row) (adjoin-position new-row k rest-of-queens)) (enumerate-interval 1 board-size))) (queen-cols (- k 1)))))) (queen-cols board-size)) ;これによって、(queens n) でサイズ n の時の盤面 (座標のリスト) のリストがえられるが、非常に見づらいので可視化する ;plot の引数 ls が盤面のリスト、再帰的に ls の頭からプロットして行き、 ls が空になったら終了 ;クイーンのいる位置を "o", いない位置を "x" であらわす ;ここで、 queens の探索順のおかげで、座標リストである盤面 (car ls) に並んでいる座標の順番は、列について降順であるはずである ;盤面を 90 度回転させたものをプロットしても同じなので、 reverse して行の昇順に並んだ座標リストとみなせばプロットが楽! ;subplot: 行をプロット ;pointplot: 座標一点をプロット ;this が今何列目をプロットしているかをあらわし、 x がクイーンは何列目にいるのかをあらわしている (define (plot ls) (if (null? ls) (display "That's all!!") (let* ((board (reverse (car ls))) (n (length board))) (define (subplot positions) (newline) (if (null? positions) (newline) (let ((position-of-queen (car positions))) (define (pointplot x this) (cond ((> this n) (subplot (cdr positions))) ((= x this) (display "o") (pointplot x (+ this 1))) (else (display "x") (pointplot x (+ this 1))))) (pointplot (car position-of-queen) 1)))) (subplot board) (plot (cdr ls)))))
[Result]
実行結果!
> (queens 4) '(((3 . 4) (1 . 3) (4 . 2) (2 . 1)) ((2 . 4) (4 . 3) (1 . 2) (3 . 1))) > (plot (queens 4)) xoxx xxxo oxxx xxox xxox oxxx xxxo xoxx That's all!!
最後に実際のチェス盤のサイズである n=8 でやってみました。92 パターンあってクッソ長かったので画像にしておきます。スクショしてつなげただけなのでそろってなくて汚いですがご了承を。対称なものは除くとかすれば面白いかもしれませんね。

EM アルゴリズムを用いた多クラス分類
[Background]
EMアルゴリズムという手法があります。気が向いたら細かい説明を載せますが、簡単に説明すると、「観測できない隠れた変数」である潜在変数を含む確率モデルにおいて、最尤解を求めるアルゴリズムです。今回はこのEMアルゴリズムを実装しました。すべてC++で実装しました。
まず、使うデータですが、三つのガウス分布から100点ずつ点を生成します。
[Code 1]
#include <iostream> #include <fstream> #include <string> #define _USE_MATH_DEFINES #include <math.h> using namespace std; // 一様乱数 double Uniform() { double ret = ((double)rand() + 1.0) / ((double)RAND_MAX + 2.0); return ret; } // 中心mu、分散sigmaのガウス分布を生成 double rand_normal(double mu, double sigma) { double z = sqrt(-2.0 * log(Uniform())) * sin(2.0 * M_PI * Uniform()); return mu + sigma * z; } int main() { string filename = "data.txt"; ofstream ofs = ofstream(filename); for (int i = 0; i < 100; i++) { double x1 = rand_normal(0.1, 0.1); double y1 = rand_normal(0.1, 0.1); double x2 = rand_normal(0.4, 0.1); double y2 = rand_normal(0.6, 0.1); double x3 = rand_normal(0.6, 0.1); double y3 = rand_normal(0.1, 0.1); ofs << x1 << "\t" << y1 << endl; ofs << x2 << "\t" << y2 << endl; ofs << x3 << "\t" << y3 << endl; } return 0; }
[Result 1]
生成した点をプロットした結果が以下の図の通りです。

[Code 2]
では実際に分類を行いますが、まずはいくつのクラスに分類するのが最も良いのかを見てみます。2~10クラスに分類してみて、それぞれにおけるすべての点の対数尤度を合計したものを見てみます。
#define _CRT_SECURE_NO_WARNINGS 1 #include <iostream> #include <string> #include <fstream> #include <vector> #define _USE_MATH_DEFINES #include <math.h> using namespace std; int main() { // number of sample const int sample = 300; // data double x[sample]; double y[sample]; // data load FILE *fp = fopen("data.txt", "r"); if (fp == NULL) return -1; for (int i = 0; i < sample; i++) { fscanf(fp, "%lf", x+i); fscanf(fp, "%lf", y+i); } string outputfilename = "likelihood.txt"; ofstream ofs = ofstream(outputfilename); for (int ncomp = 2; ncomp < 11; ncomp++) { // def paramaters vector<double> pi(ncomp, 1.0 / ncomp); double mux[sample]; double muy[sample]; for (int z = 0; z < ncomp; z++) { mux[z] = ((double)rand() + 1.0) / ((double)RAND_MAX + 2.0); muy[z] = ((double)rand() + 1.0) / ((double)RAND_MAX + 2.0); } vector<double> sigma(ncomp, 1); double Qdef = 10; double beforeQ = -10000; // EM algorithm while (Qdef > 0.001) { // E step vector<vector<double> > w(ncomp, vector<double>(sample)); double Q = 0; for (int z = 0; z < ncomp; z++) { for (int h = 0; h < sample; h++) { double sum = 0; for (int zz = 0; zz < ncomp; zz++) { double dis = (x[h] - mux[zz]) * (x[h] - mux[zz]) + (y[h] - muy[zz]) * (y[h] - muy[zz]); sum += exp(-dis / (2 * sigma[zz])) / sigma[zz]; } double dis = (x[h] - mux[z]) * (x[h] - mux[z]) + (y[h] - muy[z]) * (y[h] - muy[z]); w[z][h] = exp(-dis / (2 * sigma[z])) / (sum * sigma[z]); Q += w[z][h] * ((-dis / (2 * sigma[z])) - log(2 * M_PI * sigma[z])) + w[z][h] * log(pi[z]); } } Qdef = Q - beforeQ; beforeQ = Q; cout << Q << endl; // M step for (int z = 0; z < ncomp; z++) { double wsum = 0; double dissum = 0; double xwsum0 = 0; double xwsum1 = 0; for (int h = 0; h < sample; h++) { wsum += w[z][h]; dissum += ((x[h] - mux[z]) * (x[h] - mux[z]) + (y[h] - muy[z]) * (y[h] - muy[z])) * w[z][h]; xwsum0 += x[h] * w[z][h]; xwsum1 += y[h] * w[z][h]; } mux[z] = xwsum0 / wsum; muy[z] = xwsum1 / wsum; sigma[z] = dissum / (wsum * 2); pi[z] = wsum / sample; } } // log likelihood double LLH = 0; for (int i = 0; i < sample; i++) { double f = 0; for (int z = 0; z < ncomp; z++) { double dis = (x[i] - mux[z]) * (x[i] - mux[z]) + (y[i]- muy[z]) * (y[i] - muy[z]); f += pi[z] * exp(-dis / (2 * sigma[z])) / (2 * M_PI * sigma[z]); } LLH += log(f); } cout << "Log Likelihood is ..." << LLH << endl; ofs << ncomp << "\t" << LLH << endl; } return 0; }
[Result 2]
横軸にクラス数、縦軸に対数尤度を取ったグラフが下のようになります。

見たところ3が最もよさそうです。(8などのほうが高そうですが、3以降は上昇が緩く飽和してそうなので、過学習を避けるためにも3に設定します。もっとも、元データを3クラスで作っていると知ってしまっているのもありますが……。)
[Code 3]
では、3クラスで分類し、学習が進んでいる様子をgifで出力するようにしてみます。gnuplot を用いて、各段階での学習した中心と分散とをpngファイルに出力するようにし、Giamを用いてgifにまとめました。(gnuplot からgif animation で出力するやり方がよくわからなかった。) 下のコードを実行するとgnuplot で実行すべきコマンドが"gnuplotcommand.txt" に出力されるので、gnuplotで load "gnuplotcommand.txt" としてやれば終わりです。
#define _CRT_SECURE_NO_WARNINGS 1 #include <iostream> #include <string> #include <fstream> #include <vector> #define _USE_MATH_DEFINES #include <math.h> using namespace std; int main() { // number of sample const int sample = 300; // data double x[sample]; double y[sample]; // data load FILE *fp = fopen("data.txt", "r"); if (fp == NULL) return -1; for (int i = 0; i < sample; i++) { fscanf(fp, "%lf", x+i); fscanf(fp, "%lf", y+i); } string outputfilename = "gnuplotcommand.txt"; ofstream gnuplot = ofstream(outputfilename); gnuplot << "set para" << endl; gnuplot << "set xrange[-0.4:1.0]" << endl; gnuplot << "set yrange[-0.4:1.0]" << endl; int ncomp = 3; // def paramaters vector<double> pi(ncomp, 1.0 / ncomp); double mux[sample]; double muy[sample]; for (int z = 0; z < ncomp; z++) { mux[z] = ((double)rand() + 1.0) / ((double)RAND_MAX + 2.0); muy[z] = ((double)rand() + 1.0) / ((double)RAND_MAX + 2.0); } vector<double> sigma(ncomp, 1); int count = 0; double Qdef = 10; double beforeQ = -10000; // EM algorithm while (Qdef > 0.001) { // E step vector<vector<double> > w(ncomp, vector<double>(sample)); double Q = 0; for (int z = 0; z < ncomp; z++) { for (int h = 0; h < sample; h++) { double sum = 0; for (int zz = 0; zz < ncomp; zz++) { double dis = (x[h] - mux[zz]) * (x[h] - mux[zz]) + (y[h] - muy[zz]) * (y[h] - muy[zz]); sum += exp(-dis / (2 * sigma[zz])) / sigma[zz]; } double dis = (x[h] - mux[z]) * (x[h] - mux[z]) + (y[h] - muy[z]) * (y[h] - muy[z]); w[z][h] = exp(-dis / (2 * sigma[z])) / (sum * sigma[z]); Q += w[z][h] * ((-dis / (2 * sigma[z])) - log(2 * M_PI * sigma[z])) + w[z][h] * log(pi[z]); } } Qdef = Q - beforeQ; beforeQ = Q; cout << Q << endl; gnuplot << "plot \"data.txt\"" << endl; for (int i = 0; i < ncomp; i++) { gnuplot << "set label " << i + 1 << " point at " << mux[i] << "," << muy[i] << endl; gnuplot << "replot [0:2*pi] " << mux[i] << "+" << sqrt(sigma[i]) << "*cos(t), " << muy[i] << "+" << sqrt(sigma[i]) << "*sin(t)" << endl; } gnuplot << "set terminal png" << endl; gnuplot << "set out \"" << count << ".png\"" << endl; gnuplot << "replot" << endl; // M step for (int z = 0; z < ncomp; z++) { double wsum = 0; double dissum = 0; double xwsum0 = 0; double xwsum1 = 0; for (int h = 0; h < sample; h++) { wsum += w[z][h]; dissum += ((x[h] - mux[z]) * (x[h] - mux[z]) + (y[h] - muy[z]) * (y[h] - muy[z])) * w[z][h]; xwsum0 += x[h] * w[z][h]; xwsum1 += y[h] * w[z][h]; } mux[z] = xwsum0 / wsum; muy[z] = xwsum1 / wsum; sigma[z] = dissum / (wsum * 2); pi[z] = wsum / sample; } count++; } return 0; }
[Result 3]

いい感じ。
プログラミング初心者が書く神経衰弱シミュレーション
[Background]
友達が神経衰弱の手数の確率分布を手計算で求めていたのでなんとなくシミュレーションプログラムを書いてしまいました。
[Code]
軽い気持ちでC++で書き始めてしまったのですが、結果Cの関数しか使いませんでした。勢いでパパッと書いてしまったので不要な部分や回り道をしている部分があるかも知れません。さらっと美しいコードが書けるように精進したいです……。
#include <iostream> using namespace std; void shuffle(int *ar, int size) { for (int i = 0; i<size; i++) { int j = rand() % size; int t = ar[i]; ar[i] = ar[j]; ar[j] = t; } } int main() { int tekazu[30]; for (int i = 0; i < 30; i++) tekazu[i] = 0; int seed; for (seed = 0; seed < 100000; seed++) { srand(seed); //0~9が二枚ずつ存在 int *field = (int*)malloc(sizeof(int)* 20); for (int i = 0; i < 20; i++) { field[i] = i % 10; } //場に存在するカード int flag = -1; //二枚目が既知のカードの時に使用 int size = 20; int *memory = (int *)malloc(sizeof(int)* 10); int count = 0; for (int i = 0; i<10; i++) { memory[i] = 0; } while (1) { int drawcardindex = rand() % size; int drawcard = field[drawcardindex]; count ++; if (size == 2) //場に存在するカードが二枚になったところで終了 break; int temp = field[size - 1]; field[drawcardindex] = temp; field[size - 1] = drawcard; shuffle(field, size - 1); if (memory[drawcard] || flag != -1) //一枚目にひいたカードが前にひいたことのあるカードのとき { if (flag != -1) drawcard = flag; int i = 0; int j = -1; while (1) { if (field[i] == drawcard) { if (j != -1) break; else j = i; } else i++; } int temp1 = field[size - 1]; int temp2 = field[size - 2]; field[i] = temp1; field[j] = temp2; field[size - 1] = drawcard; field[size - 2] = drawcard; shuffle(field, size-2); size = size - 2; flag = -1; } else { int nextdrawcardindex = rand() % (size - 1); int nextdrawcard = field[nextdrawcardindex]; //二枚目をひく if (nextdrawcard == drawcard) //二枚目が一枚目と同じカードのとき { int temp1 = field[size - 2]; field[nextdrawcardindex] = temp1; field[size - 2] = nextdrawcard; size = size - 2; shuffle(field, size); } else if (memory[nextdrawcard]) //二枚目が既知のときは、次の一枚目にそのカードをひく { memory[drawcard] ++; flag = nextdrawcard; } else { memory[drawcard] ++; memory[nextdrawcard] ++; } } } tekazu[count]++; free(memory); free(field); } for (int i = 0; i < 30; i++) { cout << i<<"\t"<<tekazu[i] << endl; } return 0; }
[Result]
結果です。

16手が最大のように見えますが、なんだか最悪でも15手という噂を聞いてしまったので不安です。