Barabasi-Albert アルゴリズムの実装

[Background]

C90 に向けての原稿を書くためにネットワークの勉強をしています。東京大学性欲研究会というサークルで日曜日東ピ24aにブースを出すのでよければお願いします。
さて、この原稿で使う Barabasi-Albert アルゴリズムというアルゴリズムがあり、その実装を行ったのですが、まず背景から説明したいと思います。ちなみにこのアルゴリズムがどう原稿に使われているかはお楽しみです。

まずネットワークの構造について説明します。ここで言うネットワークは"グラフ"という言葉 (円グラフや棒グラフのグラフではなくグラフ理論のグラフです。後ほど説明します。) とほぼ同義だと思ってください。グラフとは、"ノード" (頂点) と"エッジ" (辺) からなる構造で、ノード間にエッジが張られています。このエッジがノード間のつながりを表すと思って良いと思います。今回は関係ありませんが、このエッジに"重み"という値がついている場合もあります。イメージとしては、駅がノードで、駅間のエッジが路線とすると、所要時間を重みとして与えることで路線図のグラフができる、みたいなもので良いと思います。 Wikipedia によるとグラフの中でも重みつきのものをネットワークと呼ぶようですが、少なくともここでは区別しません。とりあえず、ノードとエッジとだけ把握しておいてください。

さて、各ノードについて、そのノードからエッジが何本でているかという値が取れます。この「何本エッジが出ているか」をそのノードの"次数"といいます。たとえばノードの間に引くエッジをランダムに選んだとすると、この次数の分布を考えると二項分布になります (めんどくさいので細かい説明は省きます。気になる人は Wikipedia でも見てください、すみません) 。
二項分布の例、Wikipedia から引用

ここで、実際の世界によく現れるネットワーク構造について考えてみます。たとえばインターネットウェブのネットワークや、生態学における捕食・被食関係、友人関係などです。これについて次数の分布を見てみると、実際には二項分布でなく、べき分布という形になっていることが知られています。

べき分布の例、Wikipedia から引用
指数分布の例、Wikipedia から引用

このように次数分布がべき分布となるようなネットワークのことを"スケールフリーネットワーク"と呼びます。「次数分布がべき分布」といわれても何のことかわかりにくいのですが、要は「次数の低いたくさんのノードと、少数の次数の高いノードが存在する」ということです。この次数の高いノードのことを"ハブ"と呼びます (ハブ空港などのハブです) 。この少数のハブが、大多数の次数の低いノードとエッジを張っててネットワークが構成されているというイメージです。このネットワークの特徴として、ランダムにノードをつぶすような攻撃に対して強いというものがあります。スケールフリーネットワークに存在するノードは大多数が低次数のノードなので、この攻撃によってランダムにつぶされるノードはほとんどが次数の低いノードとなり、ネットワークの構造が保たれやすいためです (もちろん、たまたま少数のハブがつぶされた場合には崩壊しますが、それは確率的には起こりにくいものです) 。このため、たとえばインターネットウェブは停電などでランダムにサーバーが落ちてしまうといった事故に強く、捕食・被食ネットワークではひとつの種が絶滅しても生き残りやすいといった強みがあります。

さて、では実世界に多いこのスケールフリーネットワークをシミュレーションで扱いたいと考えたときに、どうやって作るかという問題が生じます。ランダムネットワークでは、ノードを作ってランダムにエッジを張ってやればよいのですが、スケールフリーネットワークを作ろうと考えた場合そうはいきません。ここで出てくるのがタイトルにある Barabasi-Albert アルゴリズムです (タイトル回収まで長かった……) 。
このアルゴリズムの概要を説明すると、まず少ないノード数 m0 (今回のシミュレーションでは2つ) で"完全グラフ" (全てのノード間にエッジが張られているグラフ、今回は2ノードなのでただの線分です) をつくります。次に、ここにひとつずつ新しいノードを付け加えます。この新しいノードから、既存のノードに対して m0 以下の本数 (今回は1本) のエッジを張ります。ここでエッジが張られる確率を、その対象となるノードの次数に比例する、とするのが Barabasi-Albert アルゴリズムです。今回は新しいノードから一本だけエッジが張られるので、既存のノードからすれば自分のノードにエッジが張られる確率は

(自分の次数) / (既存のノード全ての次数の和)

となります。

直感的には、「すでにたくさんのノードが張られている "ハブ" 」についてはさらにエッジが張られやすいので、 "ハブ" の構造が維持されやすいということになります。

[Result]

1000個のノードを作ったグラフです。割ときれいにハブが存在するのが見えると思います。

200000個のノードでも作ってみましたが、さすがに大きすぎてグラフは載せられないので、次数に対してノードの数を取ったグラフを載せます。二枚目は縦軸･横軸ともにその log を取った両対数プロットです。

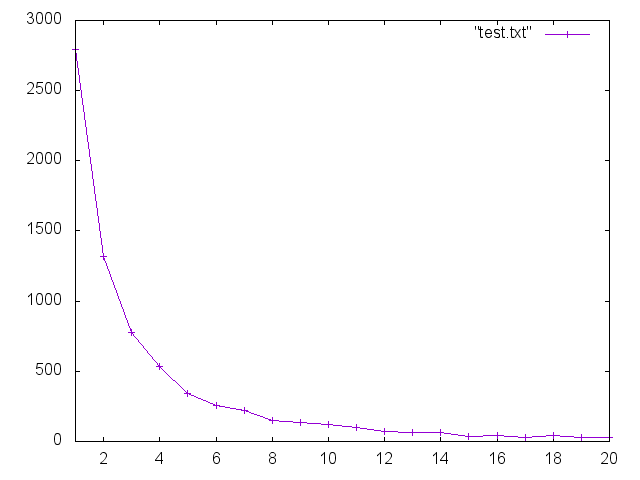
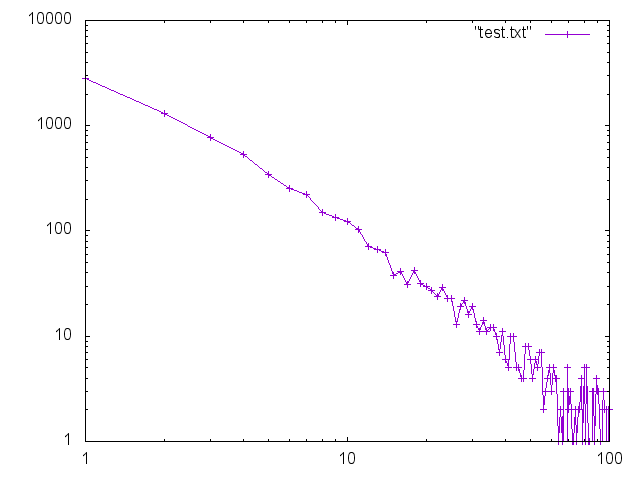
指数分布 (y = e^ax) でなくべき分布 (y = x^r) というかたちなので、ただ縦軸だけを log にしても直線にはなりません。 log(y) = r log(x) となるので両対数が正解です！二枚目が直線に近くなっているのでちゃんとスケールフリーネットワークになっていることが確認できます！

こうしてみてみるとグラフの見た目がなんとなく梅の花に見えますね。ここからは根拠のない妄想なのですが、梅の花は多分構造的にフラクタルなので次数分布がべき乗にのりそうで、グラフ化してみてみるとスケールフリーネットワークになっている、みたいなことがあるかも知れません。確かめてみると面白いかもしれませんね。

C90 では今回作ったハブの構造を持つネットワークを用いてごにょごにょいじったシミュレーションを行います。気になった方はぜひよろしくお願いします！！！！続きはビッグサイトで！！！！！！！！！！！

[追記！]

指数分布とべき分布とを混同していたので160717に訂正を加えました！訂正箇所は赤文字にしています。

[Code]

(10/25 追記) コード内の変数にある "order" は次数のつもりで使っていますが、"order" は「位数 (グラフの頂点数)」です。次数は "degree" です。訂正します。

#include <iostream>
#include <vector>
#include <algorithm>
#include <fstream>

#define N 200000			// the number of nodes
#define MAXORDER 500	// maximum order a node can have

using namespace std;

struct node
{
	int number;
	int order;

	vector<node*> adj;	// vector of pointers to adjacent nodes

	void link(node&);
};

void node::link(node& n)
{
	adj.push_back(&n);
	n.order++;
}

void annual_link(node& n1, node& n2)
{
	n1.link(n2);
	n2.link(n1);
}

struct population
{
	node* list;		// array of the nodes
	int ordersum;
	int size;
};


#define N0 2	// initial number of complete graph for BA


void BarabasiAlbert(population &population, int n)	// the argument n is the number of nodes
{
	int n0 = N0;

	population.list = new node[n];

	/* start with complete graph */
	for (int i = 0; i < n0; i++)
		population.list[i].order = 0;
	for (int i = 0; i < n0; i++)
	{
		population.list[i].number = i;
		for (int j = i + 1; j < n0; j++)
			annual_link(population.list[i], population.list[j]);
	}

	for (int i = 0; i < n0; i++)
		population.ordersum += population.list[i].order;
	population.size = n0;
	/* end of making complete graph */

	/* add the nodes from n0-th to N-th */
	for (int i = n0; i < n; i++)
	{
		population.list[i].order = 0;
		population.list[i].number = i;

		int r = rand() % population.ordersum;

		int k = 0;
		while (r >= 0)
		{
			r -= population.list[k].order;
			k++;
		}

		k--;

		annual_link(population.list[k], population.list[i]);
		population.ordersum += 2;
		population.size++;

		if (i % 100 == 0)
			cout << i << "is done!" << endl;
	}
}
#undef N0


/* population to dot format */
void dotoutput(ofstream ofs, population p)
{
	ofs << "graph graph_name{ \n graph[\n" << endl;
	ofs << "dpi = \"480\", \n layout = sfdp\n ];" << endl;
	ofs << "node[\n shape = point,\n fillcolor = \"#FF0000\",\n color = \"#FF0000\",\n fixedsize = true, \n width = 0.02\n]; " << endl;

	for (int i = 0; i < p.size; i++)
	{
		for (int j = 0; j < p.list[i].order; j ++)
		if (i < p.list[i].adj[j]->number)
		{
			ofs << i << "--" << p.list[i].adj[j]->number << ";" << endl;
		}
	}
	ofs << "}" << endl;
}



#define SEED 1
int main()
{
	srand(SEED);

	population population;
	population.ordersum = 0;
	population.size = 0;
	BarabasiAlbert(population, N);

	// check
	int order[N];
	int ordernum[MAXORDER] = {};

	for (int i = 0; i < N; i++)
	{
		order[i] =  population.list[i].order;
		ordernum[order[i]] ++;
	}
	sort(order, order + N);

	ofstream ofs("test.txt");
	ofstream logofs("log.txt");
	for (int i = 1; i < MAXORDER; i++)
	{
		ofs << ordernum[i] << endl;
		logofs << log10(ordernum[i]) << endl;	// the increment is for avoidance of negative infinity
	}

	
	dotoutput(ofstream("graph.dot"), population);
	return 0;
}